If you've been programming for long enough, you've probably heard the term dynamic programming. Often a key subject in technical interviews, the idea will also come up in design review meetings or regular interactions with fellow developers. This essay will examine what dynamic programming is and why you would use it. I'll be illustrating this concept with specific code examples in Swift, but the concepts I introduce can be applied to your language of choice. Let's begin!
A way of thinking
Unlike specific coding syntax or design patterns, dynamic programming isn't a particular algorithm but a way of thinking. Therefore, the technique takes many forms when it comes to implementation.
The main idea of dynamic programming is to consider a significant problem and break it into smaller, individualized components. When it comes to implementation, optimal techniques rely on data storage and reuse to increase algorithm efficiency. As we'll see, many questions in software development are solved using various forms of dynamic programming. The trick is recognizing when optimal solutions can be devised using a simple variable or require a sophisticated data structure or algorithm.
For example, code variables can be considered an elementary form of dynamic programming. As we know, a variable's purpose is to reserve a specific place in memory for a value to be recalled later.
//non-memoized function
func addNumbers(lhs: Int, rhs: Int) -> Int {
return lhs + rhs
}
//memoized function
func addNumbersMemo(lhs: Int, rhs: Int) -> Int {
let result: Int = lhs + rhs
return result
}
While addNumbersMemo above does provide a simple introduction, the goal of a dynamic programming solution is to preserve previously seen values because the alternative could either be inefficient or could prevent you from answering the question. This design technique is known as memoization.
Code challenge—Pair of numbers
Over the years, I've had the chance to conduct mock interviews with dozens of developers preparing for interviews at top companies like Apple, Facebook, and Amazon. Most of us would be happy to skip the realities of the dreaded whiteboard or take-home coding project. However, the fact is that many of these brain-teaser questions are designed to test for a basic understanding of computer science fundamentals. For example, consider the following:
/*
In a technical interview, you've been given an array of numbers and you need to find a pair of numbers that are equal to the given target value. Numbers can be either positive, negative, or both. Can you design an algorithm that works in O(n)—linear time or greater?
let sequence = [8, 10, 2, 9, 7, 5]
let results = pairValues(sum: 11) = //returns (9, 2)
*/
As developers, we know there are usually multiple ways to arrive at a solution. In this case, the goal is knowing which numbers should be paired to achieve the expected result. As people, it's easy for us to quickly scan the sequence of numbers and promptly come up with the pair of 9 and 2. However, an algorithm will need to either check and compare each value in the sequence or develop a more streamlined solution to help us find the values we are seeking. Let's review both techniques.
A brute force approach
Our first approach involves looking at the first value, then reviewing each subsequent value to determine if it will provide the difference needed to solve the question. For example, once our algorithm checks the value of the first array item, 8, it will then scan the remaining values for 3 (e.g., 11 - 8 = 3). However, we can see the value of 3 doesn't exist, so the algorithm will repeat the same process for the next value (in our case, 10) until it finds a successful matching pair. Without going into the details of big-O notation, we can assume this type of solution would have an average runtime of O(n ^ 2)time or greater, mainly because our algorithm works by comparing each value with every other value. In code, this can be represented as follows:
let sequence = [8, 10, 2, 9, 7, 5]
//non-memoized version - O(n ^ 2)
func pairNumbers(sum: Int) -> (Int, Int) {
for a in sequence {
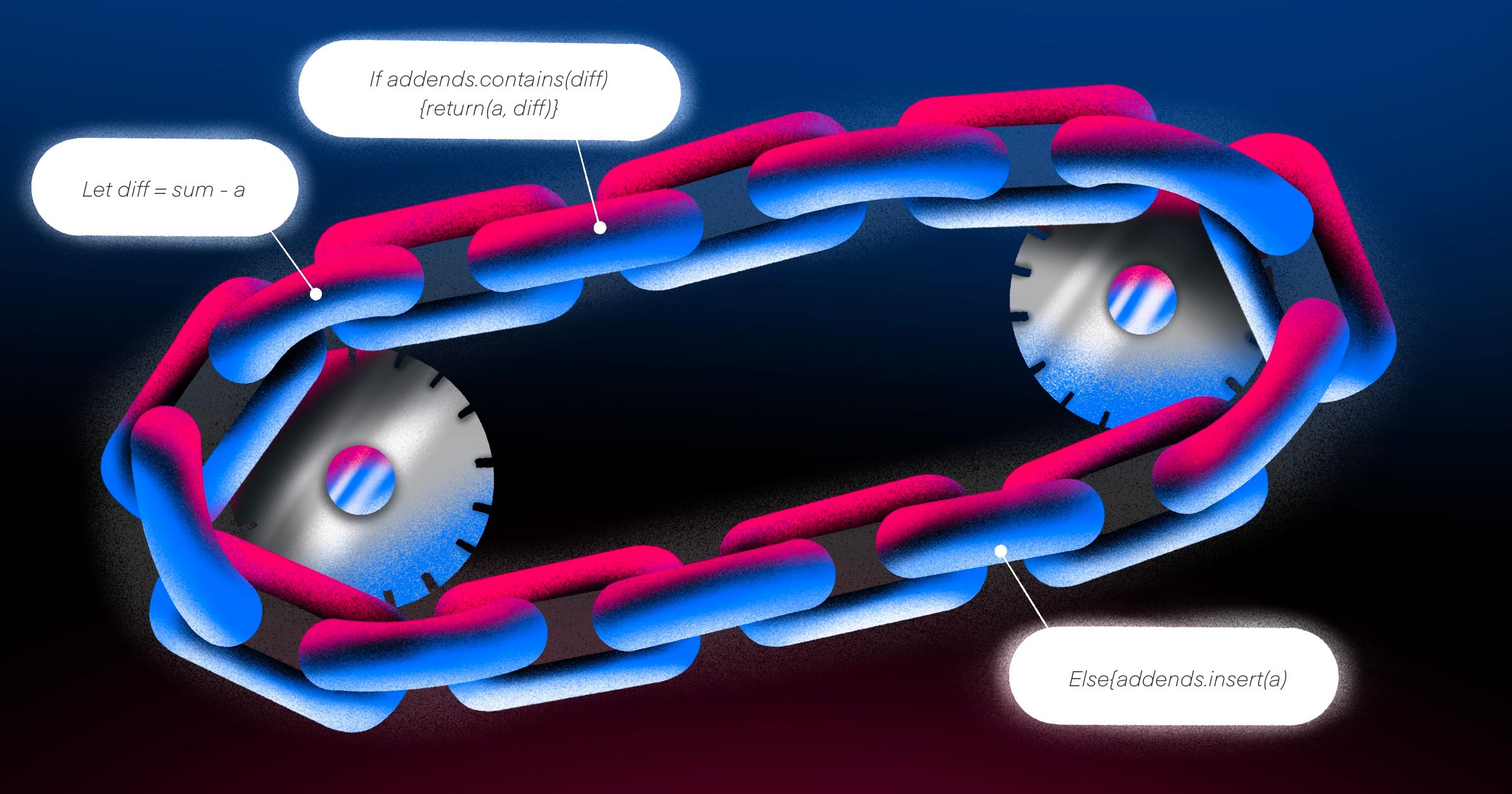
let diff = sum - a
for b in sequence {
if (b != a) && (b == diff) {
return (a, b)
}
}
}
return (0, 0)
}
A memoized approach
Next, let's try a different approach using the idea of memoization. Before implementing our code, we can brainstorm how storing previously seen values will help streamline the process. While using a standard array is feasible, a set collection object (also referred to as a hash table or hash map) could provide an optimized solution.
//memoized version - O(n + d)
func pairNumbersMemoized(sum: Int) -> (Int, Int) {
var addends = Set<Int>()
for a in sequence {
let diff = sum - a
if addends.contains(diff) { //O(1) - constant time lookup
return (a, diff)
}
//store previously seen value
else {
addends.insert(a)
}
}
return (0, 0)
}
Using a memoized approach, we've improved the algorithm's average run time efficiency to O(n + d) by adding previously seen values to a set collection object. Those familiar with hash-based structures will know that item insert and retrieval occurs in O(1) - constant time. This further streamlines the solution, as the set is designed to retrieve values in an optimized way regardless of size.
The Fibonacci sequence
When learning various programming techniques, one topic that comes to mind is recursion. Recursive solutions work by having a model that refers to itself. As such, recursive techniques are implemented through algorithms or data structures. A well-known example of recursion can be seen with the Fibonacci sequence—a numerical sequence made by adding the two preceding numbers (0, 1, 1, 2, 3, 5, 8, 13, 21, etc):
public func fibRec(_ n: Int) -> Int {
if n < 2 {
return n
} else {
return fibRec(n-1) + fibRec(n-2)
}
}
When examined, our code is error-free and works as expected. However, notice a few things about the performance of the algorithm:
Positions (n)fibRec() - Number of times called214510109151219
As shown, there's a significant increase in the number of times our function is called. Similar to our previous example, the algorithm's performance decreases exponentially based on the input size. This occurs because the operation does not store previously calculated values. Without access to stored variables, the only way we can obtain the required (preceding) values is through recursion. Assuming this code is used in a production setting, the function could introduce bugs or performance errors. Let's refactor the code to support a memoized approach:
func fibMemoizedPosition(_ n: Int) -> Int {
var sequence: Array<Int> = [0, 1]
var results: Int = 0
var i: Int = sequence.count
//trivial case
guard n > i else {
return n
}
//all other cases..
while i <= n {
results = sequence[i - 1] + sequence[i - 2]
sequence.append(results)
i += 1
}
return results
}
This revised solution now supports memoization through the use of stored variables. Notice how the refactored code no longer requires a recursive technique. The two most previous values are added to a result, which is appended to the main array sequence. Even though the algorithm's performance still depends on the sequence size, our revisions have increased algorithmic efficiency to O(n) - linear time. In addition, our iterative solution should be easier to revise, test and debug since a single function is added to the call stack, thus reducing complexities with memory management and object scope.
Conclusion
We've learned that dynamic programming isn't a specific design pattern as it is a way of thinking. Its goal is to create a solution to preserve previously seen values to increase time efficiency. While examples include basic algorithms, dynamic programming provides a foundation in almost all programs. This includes the use of simple variables and complex data structures.