If you've been programming for long enough, you have heard about the concept of a graph. It’s required content for a degree in computer science, and many top-level companies test for an understanding of graph theory during technical interviews. However, you don’t need to be working on advanced problems to utilize the concepts. Let’s review why graphs are popular data structures and how you can implement them in code.
Relational models
Regardless of coding experience, you should be familiar with the data types of arrays and dictionaries. These collections are standard concepts used in most languages and work great when presenting list-based content:

Most times, lists are the perfect solution for presenting information from a database or a REST-based query. However, there are times when a list needs to provide context as to how records relate to each other. This is when organizing data as a graph becomes handy.
With graphs, the primary objective isn't to list information (although entirely possible) but to define the relationship between objects. Why would that be useful?

Mapping applications: How would you organize data needed to recreate a mapping service like Apple or Google Maps if asked in a technical interview? More than just providing a list of all known roads in a database, your model would need to determine the best way to reach a destination based on the time of day, traffic, and one-way streets among other factors. For this considerable volume of data to be effective, you need to know how a single road relates to all other streets in the model.
Social media:Success on social media is often measured by the number of people you follow or that follow you. Networking platforms like Twitter attract massive audiences by allowing you to connect with anyone, permitting you to receive their latest updates. The LinkedIn model is more detailed as you cannot add someone to your network unless the receiver accepts your connection request. In this case, LinkedIn connections represent two-way relationships. Taking this idea further, you can also search to see if anyone in your network is connected to a job opportunity you want to pursue. In this case, "network" could imply a direct or indirect connection. Such a robust model isn't just based on a simple list but would include the smarts to determine how all profiles relate.
Graph components
Now that we've seen how graphs are used in everyday applications let's introduce their components. Nodes in a graph are referred to as vertices. While it would be possible to build a graph as a single vertex, models that contain multiple vertices better represent real-world applications. Graph objects relate to one another through connections called edges. Depending on your requirements, a vertex could be connected to one or more things through edges. It's also possible to create a vertex without edges. Finally, unlike other standard structures like stacks or queues, graphs often have no designated start or end point. Here are some example graph configurations:

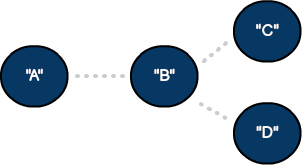
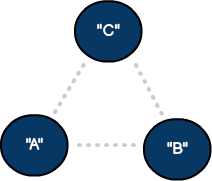
Directed vs. undirected
In an undirected graph, the connection between a source vertex and destination are equal. These models represent two-way connections—similar to a two-way street in the mapping application. To define a connection going a single direction, we can update our model to a directed graph by using lines and arrows:
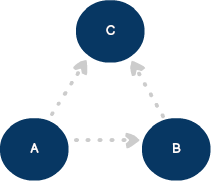
Level of connectedness
Sometimes, we must represent the level of connectedness between vertices in a graph. This technique works well when quantifying distances, times, or severity between nodes. Generally associated with an edge, the weight is a comparative variable tracked for this purpose.
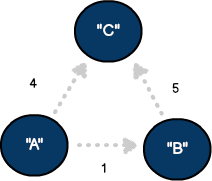
Graph vertex
With a basic understanding of graph theory in place, let's see how to replicate some of these models in code. Below we've created a vertex that supports a custom generic object (T). The tvalue variable represents the data held by the type, including a single string, int, or custom type (for example., street name or social media profile). Also, note our class conforms to the popular Equatable protocol (Swift). This will allow us to compare specific vertex instances for equality if required.
public class Vertex <T> : Equatable {
var tvalue: T?
var neighbors = Array<Edge<T>>()
let uuid = UUID()
public init(with name: T) {
self.tvalue = name
}
//equatable conformance
public static func == (lhs: Vertex, rhs: Vertex) -> Bool {
return lhs.uuid == rhs.uuid
}
}
Adjacency lists
The neighbors property represents the connections made to other vertices. As discussed, each vertex can connect to one or more neighbors. This list of relationships is sometimes called an “adjacency list” and can be used to solve many advanced problems.
var neighbors = Array<Edge<T>>()
Graph edge
We added a neighbor property to store an array of custom edge types when creating our vertex. Below, an edge provides a reference for a subsequent neighboring vertex and its potential edge weight value.
public class Edge <T> {
var neighbor: Vertex<T>
var weight: Int
init() {
weight = 0
self.neighbor = Vertex<T>()
}
}
Building the canvas
With our vertex and edge objects in place, we can now add them to our central storage structure we'll call the graph canvas. Even though our canvas is technically an array, the goal is to visualize the collection as a set of relationships. The addVertex function allows us to add a single generic vertex to the canvas, while the addEdge method provides reference information needed for an edge. Lastly, our code assumes the graph is directed, as the edge is (only) added to the source vertex adjacency list.
public class Graph <T> {
var canvas: Array<Vertex<T>>
public init() {
canvas = Array<Vertex>()
}
//add vertex to graph canvas
public func addVertex(element: Vertex<T>) {
canvas.append(element)
}
/add edge
public func addEdge(source: Vertex<T>, neighbor: Vertex<T>, weight: Int) {
//create a new edge
let newEdge = Edge<T>()
//connect source vertex to neighboring edge
newEdge.neighbor = neighbor
newEdge.weight = weight
source.neighbors.append(newEdge)
}
}
In summary, we've introduced graphs and have seen how they are used to represent the relationship between objects. We also reviewed a few ways to configure a graph and the components used to describe different models. With our model defined, we've set the stage for more advanced functionality, including graph navigation and traversal algorithms like breadth-first search.
