The big picture: Large language models are based upon a deep neural network architecture called a decoder-only transformer. Within each layer of this model, we have two key components:
1. Masked self-attention learns relationships between tokens/words.
2. Feed-forward transformation individually transforms the representation of each word.
These components are complementary—attention looks across the sequence, while feed-forward transformations consider each token individually. When combined together, they allow us to learn complex patterns from text that power the AI applications that are so popular today.
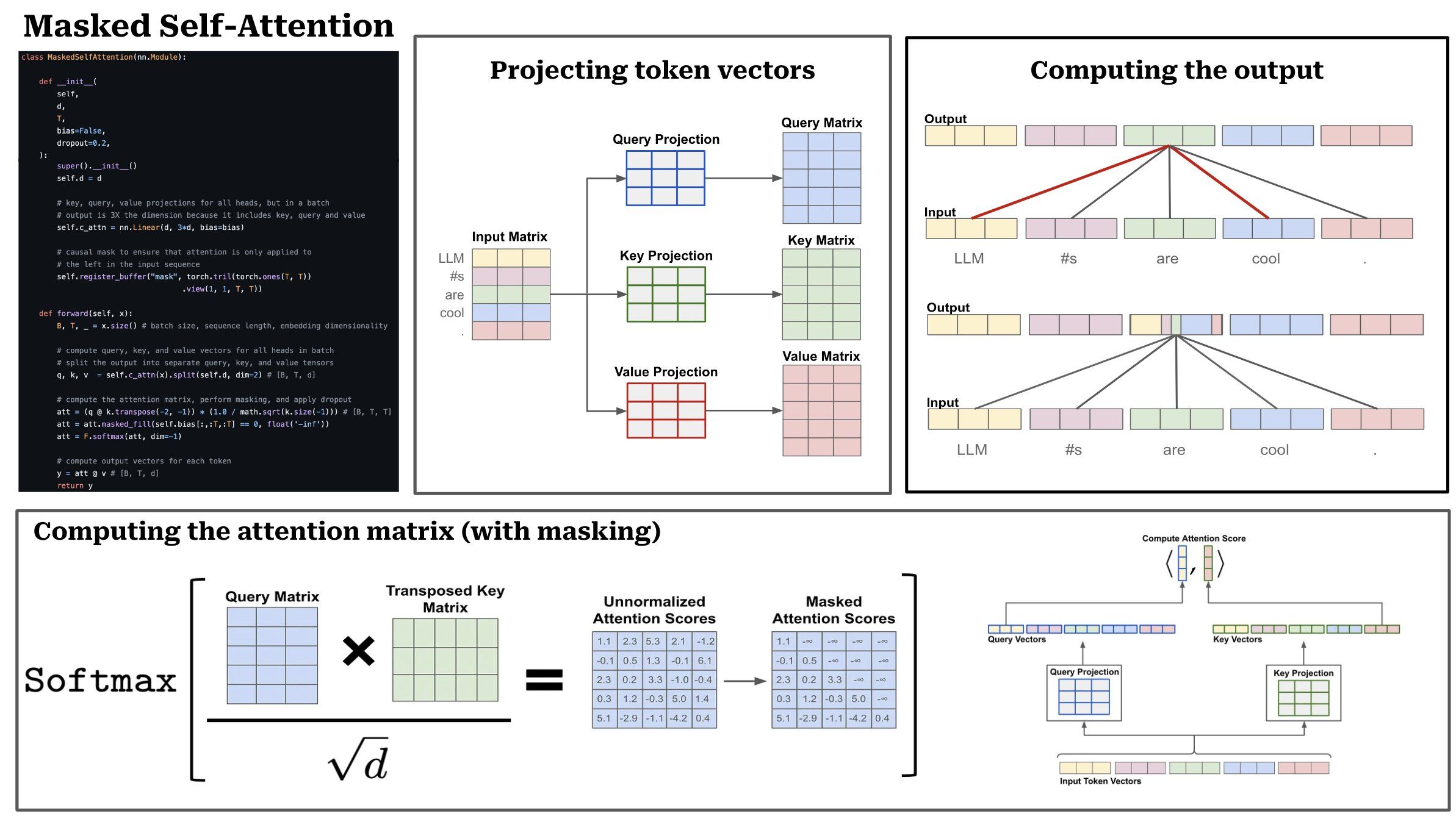
TL;DR: The input to an attention model is a list of token/word vectors, which can be stacked together to form a matrix. Causal self-attention operates by computing an attention/importance score between each pair of tokens/words in a sequence. Then, the output of self-attention is a weighted combination of all words in the sequence, where the weight is given by the attention score. We can break the process of masked self-attention into a sequence of five steps.
(1) Linear projections: The first step is to perform three separate linear projections, called the query, key, and value projections. Practically, these projections take our sequence of token vectors as input and produce three transformed sequences of token vectors as output.
(2) Attention scores: To compute attention scores, we use the query and key vectors produced by the linear projections described above. The attention score between the i-th token and the j-th token in the sequence is given by the dot product of the i-th query vector and the j-th key vector. To compute all of these pairwise scores efficiently, we can stack the query/key vectors into matrices and take the matrix product of the query matrix with the transposed key matrix. The output is a TxT attention matrix, where T is the length of the input sequence (in tokens). To improve training stability, we also divide the values of the attention matrix by the square root of the size of the token vectors (i.e., scaled dot product attention).
(3) Forming a probability distribution: From here, we can turn the attention scores for each token into a probability distribution by performing a softmax operation across each token’s attention scores for the sequence. In practice, this is done via a softmax operation across each row of the attention matrix. After this, each row of the attention matrix becomes a probability distribution that represents the (normalized) attention scores for a single token across the sequence (i.e., the i-th row contains the i-th token’s attention scores).
(4) Masking operation: In vanilla self-attention, each token is allowed to compute attention scores for all tokens in the sequence. In masked self-attention, however, we mask attention scores for any token that follows a given token in the sequence. We can implement this by simply masking the attention matrix prior to performing the softmax (i.e., fill entries for any invalid attention scores with a value of negative infinity), such that the probability of any future token in the sequence becomes zero. For example, the i-th token in the sequence would have an attention scores of 0 for tokens i + 1, i + 2, and so on. Practically, masked self-attention prevents us from looking forward in the sequence when computing a token’s representation.
(5) Computing the output: From here, we can compute the output of masked self-attention by taking the matrix product of the attention matrix and a matrix of value vectors. This operation computes the output for the i-th token by taking a weighted combination of all value vectors, where the weights are given by token i’s attention scores.